বোর পরমাণু মডেল এবং সীমাবদ্ধতাসমূহ
বোর পরমাণু মডেল এবং সীমাবদ্ধতাসমূহ (Bohr’s Atom Model)
পরমাণুর গঠন এবং একই সাথে পারমানবিক বর্ণালী ব্যাখ্যার জন্য নীলস্ বোর (Neils Bohr) ১৯১৩ খ্রিস্টাব্দে তাঁর বিখ্যাত পরমাণু মডেল প্রকাশ করেন। বোর পরমাণু মডেলটি বিজ্ঞানী ম্যাক্স প্লাঙ্কের বিকিরিত শক্তির কোয়ান্টাম তত্ত্বের উপর প্রতিষ্ঠিত। বোর পরমাণু মডেলের স্বীকার্যসমূহ নিম্নরূপ তিনটি প্রধান ভাগে বিভক্তঃ
(১) ইলেক্ট্রনের স্থির কক্ষপথ বা শক্তিস্তরের ধারণাঃ পরমাণুর কেন্দ্রস্থলে পরমাণুর সমস্ত ধনাত্মক চার্জ ও প্রায় সমস্ত ভর কেন্দ্রীভূত; একে পরমাণুর নিউক্লিয়াস বলা হয়। নিউক্লিয়াসকে কেন্দ্র করে কয়েকটি নির্দিষ্ট শক্তির বৃত্তাকার কক্ষপথেই ধনাত্মক চার্জের সমসংখ্যক ইলেক্ট্রনসমূহ নিউক্লিয়াসের চারদিকে আবর্তন করে। এই আবর্তনের সময় ইলেক্ট্রনের গতি সাধারণ পদার্থবিদ্যার সব নিয়ম মেনে চলে। তবে যতক্ষণ তা একটি কক্ষে অবস্থান করবে, ততক্ষণ তা কোন শক্তি বিকিরণ বা শোষণ করবে না। এই কক্ষপথসমূহকে স্থির কক্ষপথ বা শক্তিস্তর বা অরবিট বলা হয়।
(২) ইলেক্ট্রনের কৌণিক ভরবেগের ধারণাঃ প্রতিটি নির্দিষ্ট কক্ষপথ বা শক্তিস্তরে আবর্তনরত ইলেক্ট্রনের কৌণিক ভরবেগ নির্দিষ্ট এবং তা h/2π এর অখণ্ড বা পূর্ণ সংখ্যার গুণীতক হবে।
অর্থাৎ mvr = n x h/2π
এখানে, m = ইলেক্ট্রনের ভর; v = ইলেক্ট্রনের সরলরৈখিক গতিবেগ;
r = কক্ষপথের ব্যাসার্ধ; vr = কৌণিক বেগ; h = প্লাঙ্কের ধ্রুবক;
n = অখণ্ড সংখ্যা অর্থাৎ 1, 2, 3, 4 প্রভৃতি পূর্ণ সংখ্যা।
n এর এসব মানের উপর ভিত্তি করে যথাক্রমে প্রথম, দ্বিতীয়, তৃতীয় প্রভৃতি কক্ষপথ নির্দেশিত হয়।
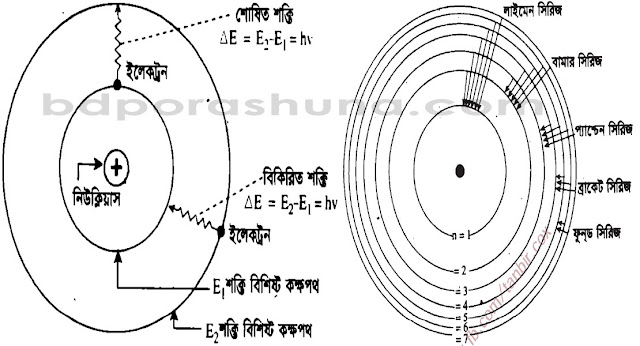
(৩) শক্তির শোষণ বা বিকিরণ ও বর্ণালী সৃষ্টির ধারণাঃ যখন কোন ইলেক্ট্রন একটি কক্ষপথ বা শক্তিস্তর হতে অন্য শক্তিস্তর বা কক্ষপথে লাফিয়ে চলে, তখন ঐ ইলেক্ট্রন দ্বারা নির্দিষ্ট পরিমাণ শক্তি শোষিত বা বিকিরিত হয়। যখন নিম্ন শক্তিস্তর হতে উচ্চ শক্তিস্তরে লাফিয়ে চলে তখন শক্তির শোষণ এবং যখন উচ্চ শক্তিস্তর হতে নিম্ন শক্তিস্তরে লাফিয়ে চলে, তখন শক্তির বিকিরণ ঘটে। যদি প্রথম কক্ষপথে ইলেক্ট্রনের শক্তি E1 এবং দ্বিতীয় কক্ষপথে ইলেক্ট্রনের শক্তি E2 হয়, তবে বিকিরিত শক্তি হবে ΔE = (E2 – E1)। এ শক্তি বিদ্যুৎ চৌম্বকীয় বিকিরণ হিসেবে নির্গত হবে। প্লাঙ্কের সূত্রানুসারে সে বিকিরণের পরিমাণ ও স্পন্দন সংখ্যা v নিম্নের সমীকরণ দ্বারা নির্ধারিত হবেঃ
ΔE = (E2 – E1) = hv
অর্থাৎ সৃষ্ট পারমাণবিক বর্ণালীতে v (নিউ) স্পন্দন সংখ্যা বিশিষ্ট একটি রেখা দেখা যাবে।
বোর পরমাণু মডেলের সীমাবদ্ধতা
বোর পরমাণু মডেলের সীমাবদ্ধতাসমূহ নিম্নরূপঃ
বর্ণালীর ব্যাখ্যাঃ প্রথমত, বোর পরমাণু মডেল হাইড্রোজেন পরমাণু ও হাইড্রোজেন সদৃশ এক ইলেক্ট্রনবিশিষ্ট আয়ন (যেমন- He+, Li2+) সমূহের বর্ণালী ব্যাখ্যা করতে পারলেও একাধিক ইলেক্ট্রনবিশিষ্ট পরমাণুসমূহের বর্ণালী ব্যাখ্যা করতে পারে না।
বর্ণালী সক্ষ্ম রেখার ব্যাখ্যাঃ দ্বিতীয়ত, এক শক্তিস্তর হতে অপর শক্তিস্তরে ইলেক্ট্রনের স্থানান্তর ঘটলে, বোর পরমাণু মডেল অনুসারে বর্ণালীতে একটি করে রেখা সৃষ্টি হওয়ার কথা। কিন্তু হাইড্রোজেন ও অন্যান্য পরমাণুসমূহের আয়নের রেখা বর্ণালী অধিকতর সূক্ষ্ম যন্ত্র দ্বারা পরীক্ষণ করলে দেখা যায়, প্রতিটি রেখার স্থানে কয়েকটি রেখা অবস্থান করছে। বোরের মতবাদে এর কোন ব্যাখ্যা নেই। অবশ্য বোর মতবাদের সম্প্রসারণ করে বিজ্ঞানী সমারফিল্ড এর ব্যাখ্যা দান করেছেন।
কক্ষপথে ইলেক্ট্রন অবস্থান ও গতিবেগঃ তৃতীয়ত, বোর মতবাদের সবচেয়ে বেশি সমালোচনা করা হয় হাইজেনবার্গ এর অনিশ্চিয়তা নীতি থেকে। বোর মতবাদে পরমাণুতে নির্দিষ্ট একই সময়ে কক্ষপথে ইলেক্ট্রনের অবস্থান ও তার গতিবেগ সুনির্দিষ্ট করা হয়েছে, যা এ হাইজেনবার্গ নীতি মতে অসম্ভব।
বোর পরমাণু মতবাদের সীমাবদ্ধতা সত্ত্বেও একথা অনস্বীকার্য যে, এ মতবাদ একটি বৈপ্লবিক মতবাদ, যা সঠিক পথের দিক নির্দেশনা করে। বোর পরমাণু মডেলের দুটি প্রধান বিষয় হলোঃ (১) পরমাণুতে বিভিন্ন শক্তিস্তর আছে এবং (২) এ শক্তিস্তরসমূহের মধ্যে ইলেক্ট্রনের স্থানান্তরের জন্য বিভিন্ন বিকিরিণ সৃষ্টি হয়, তার স্পন্দন সংখ্যা v = (E2 – E1)/h দ্বারা নির্ধারিত হয়; এ দুটি বিষয় আজ সন্দেহাতীতভাবে প্রমাণিত।











কোন মন্তব্য নেই